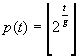 .
.
by
J. Storrs Hall, PhD.*
Institute for Molecular Manufacturing,
123 Fremont Ave., Los Altos, CA 94022
*E-mail: josh@imm.org
Web page: http://www.imm.org/HallCV.html
This is a draft paper for the
Sixth
Foresight Conference on Molecular Nanotechnology.
The final version has been submitted
for publication in the special Conference issue of Nanotechnology.
To achieve the levels of productivity that are one of the desirable prospects of a molecular manufacturing technology, the techniques of self-reproduction in mechanical systems are a major requirement. Although the basic ideas and high-level descriptions were introduced by von Neumann in the 1940's, no detailed design in a mechanically realistic regime ("the kinematic model") has been done. In this paper I formulate a body of systems analysis to that end, and propose a higher-level architecture somewhat different than those heretofore seen, as a result.
Without the productivity provided by self-replication, molecular manufacturing, specifically robotic mechanosynthesis, would be limited to microscopic amounts of direct product. Self-replicating systems thus hold the key to molecular engineering for structural materials, smart materials, the application of molecular manufacturing to power systems, user interfaces, general manufacturing and recycling, and so forth.
The cellular machinery of life seems to be an existence proof for the concept of self-replication. Indeed, many proposed paths to nanotechnology involve using it directly. However, it is limited in types and specificity of reactions as compared with mechanosynthesis, and thus in the speed, energy density, and material properties of its outputs.
Alternatively, one could select from the existing productive machinery of the industrial base, augmented with robotics to close a cycle in which factories build parts, which other factories build into robots, which build factories and mine raw materials. This is the approach of the 1980 NASA Summer Study (Frietas [1980]). This is clearly a useful avenue of inquiry; but the proposed system is very complex and is based on bulk manufacturing techniques.
It seems likely that there are simpler and more direct architectures for self-reproducing machines, ones dealing in eutactic mechanosynthesis, rigid diamondoid structures, stored-program computers, and so forth. There is, however, a really remarkable lack of even one detailed design in what von Neumann called the "kinematic model". (see Friedman (1996) vis a vis Burke (1966)). (There is no lack of designs in various cellular automata, and other "artificial life" schemes, but those have all abstracted far enough away from the problems of real-world construction that they are not directly relevant to the the design of actual manufacturing systems.)
Note that in the following I will adopt the terminology of Sipper (1997), who distinguishes reproduction, involving the exchange of genetic information and other variation strategies to allow for evolution, and replication, which does not and can be a completely planned, deterministic procedure. I will be concerned only with replication.
Consider a system composed of a population of replicating machines. Each machine consists of control and one or more "operating units" capable of doing primitive assembly operations (e.g. mechanochemical deposition reactions). Let us define the following:
p(t) -- population at time t
g -- generation time (seconds to replicate)
a -- "alacrity" primitive assembly operations
per second
s -- size in primitive operations to construct
n -- number of primitive operating units
Then ![]() and
and 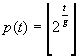 .
.
There are some interesting implications of even so simple a model.
First, if a replicator based on a single universal constructor is redesigned
to have to cooperating constructors so it builds twice as fast, but in
doing so it is made twice as complex, the growth rate is unchanged. On
the other hand, suppose the architecture is enhanced by adding constructors
that are special-purpose and thus both simpler and faster. As long as all
units can be kept busy, na increases faster than s, decreasing
g. Therefore there is no use for raw parallelism in a replicator,
but specialization (the assembly line) can be a viable optimization technique.
Assuming that the replicators can be diverted at any point to perform
at full efficiency on some task of size ST, the total time to finish
the task can be given as a function of the number of generations allowed
to complete before the diversion:
Let us consider tradeoffs between architectures at various levels of complexity. To highlight the phenomena of interest, I will describe systems at the extremes of a spectrum. Suppose we have plans for two possible replicating systems, one simple and one complex. The simple one consists of a robot arm and a controller which is just a receiver for broadcast instructions (such as described by Merkle (1996)). The complex one consists of ~100 molecular mills that are assemply lines for gears, pulleys, shafts, bearings, motors, struts, pipes, self-fastening joints, and so forth; its architecture also includes conveyors and general-purpose manipulators for putting parts together.
Drexler's nanomanipulator arm (Drexler 1992, p. 400 et seq) is 4x106 atoms without base or gripper or working tip (or motors). With the addition of motive means, a controller, and some mechanism for acquiring tools for mechanosynthesis, it seems very unlikely that a simple system could be built at less than 1x107 atoms. The arm will need a precision of approximately 1x104 steps across its working envelope to build itself and controller by direct-in-place deposition reactions. Let us assume that it takes an average of 1x104 steps per deposition, including the time to discard and refresh tools. Let us assume that it can receive 1x106 instructions per second, and can take one step per instruction.
One could design a faster arm, e.g. with internal controllers, but it would be more complex, and we are delineating an extreme of the design space here. Similarly, one could probably get by with fewer steps across the envelope, but the simplest way to achieve positional stability is to gear the arm down until the step size is small compared to other sources of error.
The simple system must execute 1x1011 steps to reproduce itself, and can do so in 1x105 seconds (about 28 hours). In order for it to reach the capability to produce macroscopic products, which we will arbitrarily define as the ability to do 1x1020 deposition reactions per second, it must have a population of 1x1018 (each individual can do 1x102), which implies 60 generations, about 69 days.
An offhand, intuitive comparison with existing industrial systems suggests that it should be possible to build special-purpose "molecular mill" mechanisms for the primitive operations that are ten times less complex than a robot arm (there are of course many such primitive operations in a given industrial machine). If we assume that stations in such a machine can be ten nanometers apart, with 1x106 atoms per station, and that internal conveyor speeds can be 10 m/s, a mill capable of building a 1e4-atom part would contain 1x1010 atoms (1x106 parts) and would produce 1x109 parts per second, or its own parts-count equivalent in a millisecond. (This is somewhat faster than the "exemplar system" of Drexler, but again we are seeking an extreme).
Suppose such systems could be built from 100 kinds of parts, and assume that we must double the complexity of the system to allow for external superstructure and fully pipelined parts assembly. Then the complex system as a whole consists of 2x1012 atoms and could reproduce itself in 2 milliseconds. Since it produces at a rate of 1x1015 atoms per second already, it needs only 17 generations, or 34 milliseconds, to reach macroscopic capability.
Given a single "hand built" simple system, we could:
This has implications with respect to an optimal overall approach to bootstrapping replicators. Suppose we have a series of designs, each some small factor, say 5.8, more complex, and some small factor, say 2, faster to replicate, than the previous. Then we optimally run each design 2 generations and build one unit of the next design. As long as we have a series of new designs whose size and speed improve at this rate, we can build the entire series in a fixed, constant amount of time no matter how many designs are in the series. (It's the sum of an arbitrarily long series of exponentially decreasing terms. Perhaps we should call such a scheme "Zeno's Factory".)
For example, with the appropriate series of designs starting from the simple system above, the asymptotic limit is a week and a half. (About 100 hours for design 1 to build design 2, followed by 50 hours for design 2 to build design 3, plus 25 hours for design 3 to build design 4, etc.) Note that this sequence runs through systems with a generation time similar to the "complex system" at about the 25th successive design. Attempts to push the sequence much further will founder on physical constraints, such as the ability to provide materials, energy, and instructions in a timely fashion. Well before then we will run into the problem of not having the requisite designs. Since all the designs need to be ready essentially at once, construction time is to all intents and purposes limited by the time it takes to design the all the replicators in the series.
This sequence has implications for the architecture of replicating systems. Since each replicator will build others of its own type for only a few generations and then build something else, a design which is optimized to allow the unitized assembler to build another exactly like itself is not optimal for the process as a whole. Similarly, a design which follows the logic of bacteria, floating autonomously in a nutrient solution, is likely not optimal.
A more efficient scheme, given the desiderata above, is to have the entire population in a common eutactic environment, and remain physically attached to each other and a substrate. The major new concern for the architecture in this approach is logistics: distributing raw materials (and information) in a controlled way, and building the infrastructure which does so and incidentally forms a framework for the ultimate product. Given such an infrastructure, productive units need not be individually closed with respect to self-replication.
This significantly relaxes the constraints on the design of any unit in a beneficial way. Current practice in solid free-form fabrication (see, e.g., Jurrens 1993) suggests that machines of moderate complexity should be considered capable of making parts smaller than themselves, but not machines their own size. This suggests a two-phase architecture consisting of
Any manufacturing system can be described by a directed graph, where each operating unit is represented by a vertex and the inputs and outputs are considered to flow along the edges. For the analysis of self-replicating systems, we must add a secondary type of edge, in addition to the ordinary product edges, which indicates that the product, instead of forming an input to its terminal vertex, is an instance of the operating unit the terminal vertex represents. We will call these secondary edges capital edges.
Each system will in general have exogenous product edges, representing the inputs to the system as a whole, and if it is to be useful, egressive product edges as well. Any real-world self-replicating system will have these inputs and outputs as well; that is to say, we do not consider a system to be non-self-replicating because it obtains raw materials, energy, or indeed control from the outside world. Instead,
Definition 1. A system is self replicating if each vertex is the terminus of an endogenous capital edge.
Note that the functions of transport as well as assembly can be represented by explicit vertices, which means that models such as von Neumann's kinematic model of an assembly robot floating in a sea of parts can be described as self-replicating in our sense:
Figure 1. A simplified von Neumann model. Capital edges are represented in red.
Note that the constructor vertex in this diagram has a self-loop capital edge. We call such vertices self-replicating kernels. Note that a system does not necessarily have to have such a kernel, but if one can be designed, it often simplifies the rest of the system. Note also that the schema conflates instances of mechanisms; it does not distinguish between units in parent and offspring systems. However, it is permissible to duplicate vertices to distinguish applications of the same unit, as in the case where the constructor used a different set of inputs to make different products; there would be separate copies of the constructor vertex with different connections.
In a standard top-down design methodology, a critical part of the specifications for a machine is its capabilities; to build a manufacturing system, for example, it is useful to know what it must manufacture. For a self-replicating system, however, the product is the system itself, the specifics of which are not known until the design is completed. Therefore the design process must be somewhat ad hoc.
In an attempt to ameliorate this situation, theoretical studies of self-replication often opt for a "universal constructor". This concept is derived by extension from "universal computer", and in the non-physical world of the cellular automaton it does seem reasonable to posit a mechanism which can produce any pattern of states in the cell space of the model. However, the use of the term in the physical world has given rise to confusion and controversy. Thus we will use instead the concept of self-replicating kernel as above, and the more explicit methodology of the producer/consumer diagrams.
Following the architecture above, we will split the notion of the general-purpose constructor into the tandem of parts fabricator and parts assembler. The parts fabricator:
There are a number of factors which motivate this architecture. First, it greatly simplifies the design of the fabricator for the object it builds to be rigid. This allows the fabricator to address reaction points on the surface of the partial object without concern for whether the object has undergone a configurational change. It relieves the fabrication design process from the necessity of scaffolding, its provision and subsequent removal, simplifying the process and making it easier to maintain a eutactic environment.
These specifications argue for a parallel robotic configuration in the case of the fabricator and a serial one in the case of the assembler. Parallel linkages, such as the Stewart platform, offer increased stiffness at the cost of decreased range, whereas serial linkages, such as an anthropic-style arm, have maximal range but low stiffness. (Note that the parallel / serial distinction is not universally useful; an X-Y table is parallel if it rides on orthogonal actuators each of which allows free motion in the other's direction, but serial if it consists of an X-table mounted on a Y-table.)
A low-precision arm can nevertheless construct objects with atomic precision by the use of guides and jigs, just as a human draftsman can draw a straight line using a ruler. Clearly, the envisioned tasks will often employ such jigs. However, the fact that the system is operating at the atomic suggests another technique. It is commonplace in biochemistry for the parts of an object (e.g. a virus) to self-assemble. We can make use of the same phenomenon.
In general, a part held at the effector of an arm will occupy a probabilistic cloud of space whose shape depends on the specific stiffnesses and degrees of freedom of the arm. If there is within the cloud an energetically favored configuration, the part will seek the configuration without additional manipulation.
The most obvious construction of such a situation consists of a part whose shape fits a complementary cavity at the desired position. The arm need only hold the part against the cavity, and let go. More elaborately, the arm can constrain some degrees of freedom of the part but allow others to follow the pathways designed into the configuration. For example, the arm holds a bolt up to a threaded hole. The bolt is not driven, but allowed to rotate freely. With the proper fit, the bolt will screw itself in.
This phenomenon can be combined with a number of techniques involving the inclusion of jigs and guides in the shapes of parts, to produce assembly procedures that involve in the most part moving an object to the right place and letting go, instead of the complex manipulation involved in the assembly of macroscopic mechanisms.
In cases where self-assembly implies a lower energy barrier to self-disassembly than is desirable, a compound sequence can be used. For example, mating parts of a frame will hold together during assembly but a self-inserting bolt will produce a significantly stronger one.
Figure 2. An interleaved joint between two struts will assemble easily and offer some strength due to van der Waals forces at the interface, but a bolt will increase its strength. In this design, the bolt is simply a threaded cylinder with no head. The fully-inserted position is the bottom of a potential well.
Other phenomena of interest include self-assisted half-assembly. A bolt as in the above example might have a resistance to movement that increased with the surface area in contact, but with a self-insertion force that was essentially constant (i.e. proportional to the derivative of area in contact). In this case the self-insertion would bog down at some point. The assembler arm could apply mechanical force to the bolt to increase the energy gradient (but would still need only push and not turn).
A final advantage to self-assisted assembly is that it simplifies the programming of (and/or volume of external instructions transmitted to) the system. For a system which ultimately comes to be composed of a very large number of robotic units, this can be a non-trivial consideration.
Given the rapid progress to date in the study of the electrical properties of nanotubes and molecular switches, it is reasonable to expect that it will be possible to build conductors and switches into the material of rigid parts even if the synthesis is entirely hydrocarbon. It is desirable to have a capability for such "printed circuits" even if it means extending the chemistry of the synthesizer. The alternatives include mechanical demultiplexers of acoustic pressure signals (Merkle, private communication). With a modest circuit capability it is possible to embed an electrical demultiplexer into the structural parts of the assembly robot. This leaves the construction of the logic in the domain of the parts synthesizer, which is outside the innermost self-replication loop, a desideratum. Alternatively, an electromechanical distributor, a combination of a relay and the rotary unit in a ball-point pen, can act as demultiplexer with only one moving part.
Figure 3. Rotor for an electro-mechanical distributor. It mates (face down) with a substrate with an identical surface, in a well which constrains it to a single rotational degree of freedom. The lands are slightly wider than the gaps, so it does not mesh with the substrate, but always rides on top. This produces the uncharged PES seen below. Embedded charges produce the charged PES in interaction with drivable electrodes in the well wall.
Figure 4. Potential energy surfaces for the distributor (as a function of rotational angle). With uncharged electrodes it will remain at (a) due to the upper blue PES (a function of its shape and van der Waals forces). An incoming pulse charges the electrodes and adds the red PES with the result of the overall lower blue one. The black line at (b) indicates the region where the conductive path for switching lines up, allowing current to flow to the appropriate output wire. When the input pulse ends, the rotor relaxes to (c) where the next pulse should induce the negative of the red PES to advance the rotor.
Figure 5. A two-phase electrostatic stepper, the core of the gearmotor below.

Figure 6. A high-reduction differential-drive gearmotor. The one pictured would have a reduction ratio of 52, but it is possible to get reductions of over 1000 with reasonable tooth numbers.
For driving the arms and so forth it is necessary to have a high-torque drive, and the easiest way to do this with rigid parts is a gearmotor. Macroscopic high-reduction gearmotors often have flexible splines or multiple stages, which are undesirable for fabrication or assembly respectively. The design shown is capable of extremely high ratios, consists of a small number of rigid parts, and can be assembled starting with the case simply by putting the parts in their places. The top internal gear is cut away to show the structure; in practice it would constitute a cap which mates with a spindle extending from the center of the bottom casing.
The essential burden of the foregoing is that is is now straightforward to design a parts-assembly robot that is, except for its motility, well within current well-understood practice of parts-assembly robots. Given a framework to move in that provides precise positioning and traction, as described below, the problem of motion control is relatively modest.
The design depicted is probably overkill, and a more effecient version is likely to emerge from further investigation. The salient features are its ability to engage, move, and turn in the framework, and the fact that it has two manipulators. Development of more careful designs with self-assisted assembly and a judicious selection of jugs and clamps may obviate the duplication and permit a one-armed design.
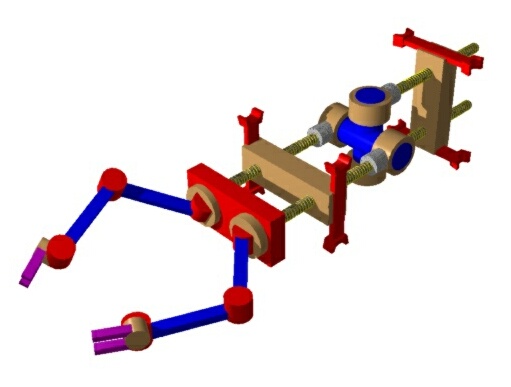
Figure 7. A motile parts-assembly robot. The outward clamps in the rear engage the struts of the framework. Early generations of robot have no on-board control but obey signals transmitted across the framework.
The parts synthesizer uses basically the same motor and control structures as the assembly robot but arranged to the effect of more precise (but thereby slower and shorter) positioning capability. In theory, a 4-position (2-phase) stepper as above with a 50-to-1 reduction driving a 2-nm pitch lead screw (i.e. 1 nm lands and 1-nm grooves) can position a slider with a precision of 0.01 nm (0.1 angstrom). This is sufficient for mechanosynthesis, and the parts can be assembled correctly by a manipulator with 25-to-50 times grosser precision.
My proposed design for a fabricator, seen below, is based loosely on a conventional milling machine. The long motion axes are all driven by lead screws, and the motions of the wrist to orient the working tip are by high-reduction-ratio steppers with short working radii.
A problem that does not appear to have been addressed heretofore is that of starting the deposition process. My proposal is "starting blocks", which would be small blocks of diamondoid material provided as raw material (just as would be working tips). The table (y in the figure below) would be tesselated with cavities of an appropriate shape to bind the starting blocks reliably. Once the part was fabricated, it would be removed from the table by the application of mechanical force by an assembly robot. The assembly robots would also position the starting blocks oroginally and provide the synthesizer with a stream of working tips in early versions. (Note that self-assisted assembly, together with appropriate jigs and limit stops, allow the robot to place the tool precisely in the synthesizer's manipulator.)
Figure 8. Parts synthesizer. An openwork truss can have a high stiffness-to-mass ratio, and can be easily assembled from smaller parts. In this design, there are three axes of motion (x, y, z) consisting of sliding dadoes driven by lead screws. There are three axes of orientation at the wrist (b) for the mechanosynthetic active tip (c). The y-slider table extends beyond the frame in the y direction (in and out of the page) but is not required to have high stiffness at its ends.

Figure 9. A more detailed view of the wrist assembly. Orange indicates motor/bearings (only one motor is required per DOF, so one of the pitch-axis joints can be an unpowered bearing). Preliminary studies indicate that the bend in the toolholder allows a greater range of access to the typical object under construction than a straight one would.
The bootstrap configuration is a small framework, one assembly robot, and a pile of parts. The robot builds parts fabricator and other robots and extends the framework. Later robots, and framework nodes made from parts from the fabricator instead of the bootstrap stock, have onboard computers. Ultimately the framework is a distributed control system coordinating the activities of large numbers of robots, as well as the physical infrastructure for the target product.
At each stage in its development, the system maintains the "self-replicating system" property. Note in the diagram below that as the system expands, it builds machinery which takes new inputs and transforms it into the old inputs. (Somewhat contradictorily, in the case of physical inputs the move is to the simpler and more numerous, whereas the control inputs move toward the more condensed and complex.)
As the system matures, it will be possible to discard the bootstrap. A mature version of this design, oddly enough, does not have a self-replicating kernel, but a two-vertex loop of assembly lines which build robots which build assembly lines.
Figure 10. System diagram for the bootstrap path of a self-replicating manufacturing system. Each subsystem in a blue line (as well as the entire system) meets the self-replicating system criterion.
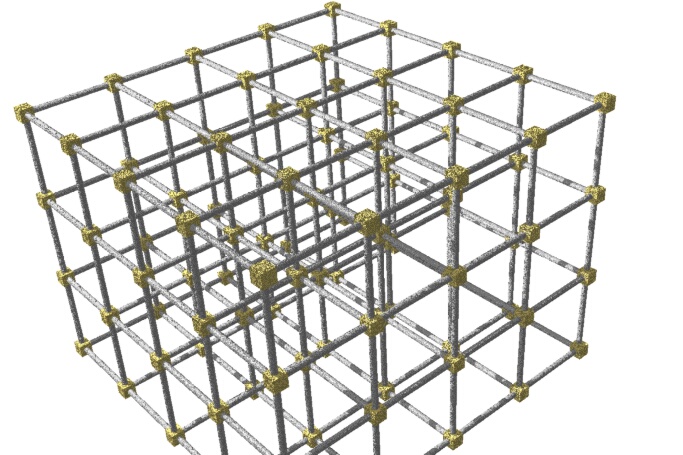
Figure 11. The framework. Ultimately the framework is a distributed control system coordinating the activities of large numbers of robots, as well as the physical infrastructure for the target product.
I have done a systems analysis for self-replicating manufacturing systems. There are several results of this analysis that have implications for their design. First, replicators do not benefit from raw internal parallelism but do benefit from concurrency of effort involving specialization and pipelining. Given the enormous range of possible replicator designs, the optimal pathway from a given (microscopic) replicator to a given (macroscopic) product generally involves a series of increasingly complex replicators. The optimal procedure for replicators of any fixed design to build a given product is to replicate until the quantity of replicators is 69% of the quantity of desired product, and then divert to building the product.
Therefore, it is desirable to design a replicator with the understanding that it will reproduce itself only for a few generations, and then build something else. Furthermore, it is crucial to design replicators that can cooperate in the construction of objects larger and more complex than themselves. I have outlined a system that embodies these desiderata.
Finally, considerations encountered in the design of the present system have convinced the author that, given a precursor or bootstrap technology (e.g. self-assembly from biomolecules) that can produce usable parts, the first thing to be built from the parts should be a parts-assembly mechanism and not a parts-fabrication mechanism. A parts-assembly robot constitutes a self-replicating kernel in an environment of parts, and a growth path that maintains the self-replicating system property (i.e. that each vertex of its diagram is the terminus of an endogenous capital edge) appears to work best.
I would like to thank K. Eric Drexler and Ralph Merkle for discussions leading to this work. Any errors or misinterpretations are of course my own responsibility.