The design of artifacts this complex presents a task so daunting that even for human designers it is broken down into a myriad parts. This is done both by levels of abstraction -- in designing a computer, for example, we may design the instruction set as a completely different activity from designing the circuitry of a pipelined floating-point unit -- or by decomposition, breaking the overall design down into parts as separate problems, e.g. in a robotic system separate people or teams design the mechanical arm, the power supply, the controller, and the software.

Even given the breakdown into subproblems, each subproblem is generally very difficult or computationally intractable. Even the problem of routing one net, a wire connecting two or more devicesacross a VLSI chip, is NP-complete (the Steiner tree problem).

But worse, the environment for which one part is designed consists of of all the other parts. They must fit physically together; they must be tightly enough coupled to transmit the desired forces, objects, signals, etc., and yet be insulated enough not to transmit undue heat, vibration, and in general reduce undesired side effects to an acceptable level. (The problem is exacerbated in a self-reproducing machine. In this case the very specifications of the machine's constructional capabilities depend on the makeup of its own parts.)

It should be clear that similar interactions take place between levels of abstraction as well as decompositional parts. One can design a gear train with the mathematical properties desired only to realize that the gears simply won't fit together. The availability of novel lower-level components (e.g. a toroidal worm gear) may inspire different higher-level designs than otherwise.

Complete optimality would thus require that while designing each part, we take full consideration of all the rest of the system. Clearly this defeats the purpose of the breakdown, and leaves us with an intractable task. Thus one of our major goals is to find a way to abstract from the rest of the system just that information that is relevant to the design of the part under consideration. Of equal importance is the ability to do this in parallel for all the parts, converging or relaxing the whole system toward optimality.

Coordination and Effort Allocation

A commonly used approach for attacking computationally intractable problems is that of exploring some space of possible solutions in a controlled random way. Techniques include random-restart iterated hillclimbing, simulated annealing, genetic algorithms, and so forth. Good results can be had with an appropriately chosen technique; more critically, the representation of the problem, and thus the space being searched, is enormously important to the success of the technique.

Our earlier research in this field have involved the control of stochastic methods in a multilevel setting. In particular, given an overall design system that is using stochastic methods in many different places, how much effort should one invest in one search as opposed to another? Using the methods of rational control (a la Russell and Wefald), we had developed analytical methods for attributing values and costs for various parts of the abstraction hierarchy, laying a basis for comparison of activity in different areas.

This method has certain drawbacks. It is global, and thus becomes unwieldy as overall system complexity increases. It requires statistical sampling, either ahead of time or as design progresses, and its dicta rest on certain assumptions about the shapes of statistical distributions. And it was formulated for an abstraction hierarchy but not a decompositional one.

We would like to have a method that is adaptive and makes as few statistical assumptions about the process as possible.

The Economic and Evolutionary Mechanisms

Of the models of well-studied real-world phenomena that have been abstracted as control algorithms for stochastic methods, two which seem to address these issues in some way are the evolutionary and the economic. Evolution produces complex designs in the face of limited resources. Economics, more specifically price theory, concerns itself with the formation of global optima (global over the distributed set of agents, not the solution space) by means of local mechanisms. It is our burden in the following to show how these models can be combined and addressed to the specific problems of multilevel, multipart design.

Price theory can be thought of as explaining that the pricing mechanism is a way of abstracting information to exactly that minimum which allows local decisions to lead to a global optimum. When one considers the problem of intractable subproblems in design, the abstraction of constraints from the rest of the overall task to a minimum is eminently desirable. Our intent is to formulate an economic model such that the price levels reflect both the value to the quality of the ultimate design, and the cost in terms of computational resources, of each alternative being considered.

Summary of Motivation and Approach

• Cost and value calculations can be local and the market mechanism propagates them automatically.
• Rather than explicit statistical estimates of distributions, populations of competing agents are adapted to market conditions by the genetic algorithm, using profitability as a fitness measure.
• Instead of a simple linear hierarchy, any pattern of computation and information flow can be supported.
• The price mechanism is used for selection of components as well as control of design effort. Since the mechanism is unified, the system should automatically decide between the use of library or stock parts, and custom design, generally resulting in a mixture in the overall product.
• It should be feasible to incorporate existing methods and knowledge. A major goal is to provide a vehicle for the coordination of as much external expert knowledge as possible. The role for the market and evolutionary mechanisms should be seen as analogous to bearings and shafts, while the motors and wheels are supplied as appropriate to the task at hand.

The system consists of a collection of "software agents" which interact by means of buying and selling objects (or services). The overall pattern of activity has great similarities with many other pluralistic cognitive architectures, including Selfridge's Pandemonium, Newell's SOAR, Holland's classifier system, Minsky's Society of Mind, and Mitchell’s Copycat. To distinguish the particulars of our software agents from the others, we will follow the economic literature and call them "firms".

Firms interact by means of a global, black-box communication system. Firms can post messages of the form, "I want to buy such-and-such", called "Wanted" messages, and "I have such-and-such to sell", called "Sale" messages. When two firms post matching offers to buy and sell, commerce can occur. The messages contain prices and specifications for the objects sought or offered. Specifications include any and all properties of the design, including level of abstraction, cost to build, size, power consumption, speed, function, tolerances, timing, and so forth.

Firms which are successful in commerce accumulate money; those unsuccessful, either by selling low and buying high, or from never engaging in commerce, lose money. New firms are created and old ones destroyed in a steady-state genetic algorithm using firms' account balances as a fitness measure. In practice the system runs in alternating phases, a commerce phase and a genetic phase.

A firm typically knows how to build something given various resources, e.g. a multi-bit adder firm would know how to put together full-adder modules; a speed reducer firm would consume gears, shafts, casings, and bearings. Each firm only knows how to do one thing: there would be separate firms specializing in ripple-carry adders, lookahead adders, carry-skip adders, etc.; and ones specializing in spur, helical, worm, planetary, harmonic, and so forth reducers. The idea is for the price and matching mechanisms to make the selection.

When there is an Wanted message that matches a firm's product imperfectly, the firm may act in entrepreneurial mode (each firm’s office is run each cycle, so this is under the individual firm’s control). It might then check the prices for the components it needs and estimates the amount of effort it must expend to meet the specs. It can either speculate by attempting a synthesis which may or may not succeed, or post a (Sale) counteroffer. The higher the price offered in the mismatch the more likely the firm is to be activated. If some of the necessary components are not offered (and thus the firm doesn't know what they will cost), it can post Wanted messages at prices for which it estimates it could profitably use the items.

The Alternating Ecocycle

The basic idea is to run a genetic algorithm over the firms where their fitness is their account balance, while at the same time running a market using whatever firms exist at the moment. We use a steady state GA, and tournament model selection for both breeding and mortality. Thus there is no strict "bankruptcy" level of debt, but debt is disadvantageous over the long run.

The problem with the simple approach to breeding in the GA is that if we require exact match in goods for transactions to occur, no business will result. That is, take two firms (specified by a vectors of parameters), and mix them in the standard "crossover" fashion. Since the firms must be able to produce their outputs given their inputs, the most we can mix is the inputs or the outputs, computing the other from the result. However, in an environment of any complexity, randomly mixed object specifications will almost never match any existing buy or sell specs.

What we do instead is to generate new firms from existing buy-and-sell advertisements. A firm might be generated from two offered goods and produce a new product, or from an offered and a sought good, generating a new wanted ad for whatever the appropriate difference might be. And of course if there are matching sets of a sought good and two offered ones that could be directly combined to form it, we want to generate firms to do the construction.

The model runs in alternating phases. In the genetic phase, we generate new firms by putting together parts of successful firms and patterns from the advertisements. We also kill off firms with low account balances.

In the opposite, agoric phase, construction and exchange occurs. First, for each different kind of good advertised (buy or sell), all the buyers and sellers are gathered into a local market and the bidding process is done (see the Appendix for details). Essentially we sort sellers by price, in ascending order, and buyers in descending order. We pair them off in order as long as the buyer's price is higher than the seller's. A price halfway between those of the last (nearest) pair is called the market price, and all exchanges are made at that price.

Firms

The major parts of a firm are as follows:

• factory. This is a procedure in the form of a function that takes zero or more inputs (arguments) and produces an output. It may be non-functional in the sense of producing different outputs when repeatedly applied to the same arguments, but it is considered atomic for any given application.
• specifications. There is a spec for each input and for the output. These are in some pattern language which is appropriate for the task at hand.
• front office. This is the algorithm that looks at the market and decides what prices to offer for inputs and ask for output. (The factory is run automatically when there are appropriate matches.)
• account. This is how much money the firm has. Rather than having banks and so forth, the firm can "borrow" by allowing the account to go negative. The account balance affects how often the firm can run.

The "office" of a firm should be fairly simple, essentially some parameters or expressions that control built-in commerce algorithms. The other items are essentially pointers, so that the firm may be instantiated many times with the same factory but different market strategies.

There are two properties of human market behavior that we would like to capture. The first is that productive behavior is imitated because it is rewarded. This expands the sector of the economy doing the productive task until the competition drives the rewards back down to the average level. The second is that good market modelling is rewarded. It is hoped that with a good formalism for the front office function, useful models of the relationship between the market and the firm's own function will develop.

It is also to be hoped that the genetic algorithm can be used to improve the factory to some degree. This is more problematical in general and clearly very idiosyncratic to specific functions. Most algorithmic synthesis and analysis functions do have some parameters which are susceptible to stochastic optimization. It is even possible to allow variations that do not guarantee a match between output and the original spec, if there is a way of modifying the spec to reflect the actual output.

A Lattice of Goods

In human markets, the price mechanism carries information, but that information is grounded in the full panoply of ontological knowledge. It does us little good to know a price if we do not know what it is the price of. In a computational market model, the language in which goods are described is thus as important, if not more so, as all the rest of the mechanism. Indeed most experiments to date, not to mention standard economic analysis, simply assume the ontology, often dealing in a single kind of completely interchangeable commodity good, or in a set of equivalence classes of such goods.

To capture the hoped-for benefits of the model as a coordination mechanism, however, we need an explicit yet flexible ontology. If the communications mechanism is going to allow them to talk about different things, our firms need a way to know what they are talking about. At the same time the space of possible objects shouldn’t be bigger than necessary, or wasted computation will result.

We have done our initial experiments on a two-dimensional bin-packing problem. (This is clearly germane to, and was inspired by, floor-planning in VLSI, but can also be viewed as a simplified version of parts layout in any physical design.) Each "problem" consists of a number of rectangular primitive modules, each with a given size and shape, which must be placed together like parts of a jigsaw puzzle to form a compact overall rectangular shape. In a slight simplification of standard practice, the construction process consists of butting sub-rectangles together and taking the smallest bounding rectangle of the result. The result can thus be described by a binary tree whose leaves are the primitive modules. Each node in the tree is accompanied by a rotation/reflection parameter (8 possiblities).

The goods, i.e. the actual concrete designs produced within our system are such trees. In order to describe them at an appropriate level of abstraction, there is a language of specifications ("specs"). Each spec consists of a vector of numbers: the area utilization quotient of the design; the height and width; and for each type of primitive module, how many instances of it are in the design.

Consider two layouts, a and b. If a contains every module that b does, and is smaller, it is a better design in some sense. If it is both shorter and narrower, it is strictly better in the sense that a can be substituted for b in any layout containing b. If we represent the height and width by their negatives, the "better than" relation is captured in the condition that all elements of a be greater than or equal to the corresponding element of b. This generates a simple and regular partial ordering of specs.

This "better than or equal" relation is the basis of commercial discourse in the present experiments, and we conjecture that something like it will be beneficial to any more elaborate scheme. When a firm advertises a spec (buy or sell), it means "some layout equal to or better than" that spec. If the Sale spec is better than the Wanted one, the object advertised is guaranteed to satisfy. The opposite is not the case. Thus the market mechanism considers sales only between firms where the Sale spec exceeds the Wanted spec.

In the current implementation, it is the responsibility of the seller to assure that the actual object matches the spec it has been advertised as. This is computationally equivalent (and more efficient) to having the buyer do it and reversing the transaction if it fails. If the transaction were not reversed, the economic burden of speculation would shift. We want it to fall on the seller, which is the locus of pricing knowledge. This enables the kind of adaptation seen in our first experiment below.

Speculation and Rational Control

Let X be a firm whose factory produces, stochasticlly, designs specified in an Wanted message. For simplicity assume X's inputs are constant in price and availability. Furthermore assume X's factory costs an average of $10 to run and produces a design that has, on average, a figure of merit (about which it only knows the value) of 53, and a standard deviation of 21.

Now suppose there is a firm C that needs a design and is willing to spend up to $100 to get the best one it can. C offers to buy designs for $1 and there are no takers, so it raises the offer. When the offer gets to $10, X accepts and sells C a design. Now C has $90 and a design with, say, a figure of merit of 51. C again offers to buy a design for $10, but now specifies that the figure of merit must exceed 51. Should X accept this offer?

Probably not, since nearly half the time the design X produces won't match and can't be sold. X should wait until C has raised the offer to $20. Then X can afford (in the long run) to lose its investment (paying for the CPU to run its factory) half the time since it will make it up the other half. For each quality cutoff there will be a price that makes it worthwhile for X to try for the offer.

It is clearly advantageous to X to know the properties of its own factory. It is also difficult, and more to the point, computationally expensive, to characterize the distribution of outputs with respect to any given input spec and fitness measure. On the other hand, in the marketplace any knowledge is better than none. Versions of X that sell too cheaply will quickly go bankrupt. Versions that charge too highly will never sell anything and go bankrupt more slowly from maintenance costs. Those in the middle will prosper. There need not be any one firm X which "knows" the whole distribution. There would instead be a population of versions whose specs gave them a niche, e.g. "run if the desired figure of merit is less than 66, and the price is over $23." This population as a whole would come to approximate to the distribution (but only in areas where there was sufficient activity to warrant it).

Note that the dynamic allows the seamless inclusion of more standard algorithmic methods. Suppose there were a method that cost $500 to run and guaranteed a quality of 98. Its "Sale" patterns are obvious. If the customer can't do better with the stochastic method, the price keeps going up and the algorithmic method runs.

The other side of rational control involves a justifiable increase in the effort to optimize a component because it will be used more than once and the development cost can be amortized. Speculative development in response to early requests for parts has many of the same properties as the speculative stochastic search just described. The "front office" is estimating how often the part will be used rather than (or perhaps in addition to) the effort needed to design it.
 

Summary of System Design

In our experiments below, the variation in "firm" subroutines was done by providing a fixed algorithm with a set of control parameters which was manipulated by the genetic algorithm.
 

We report here on three sets of experiments testing increasingly complex aspects of the system. Our first experiments were to determine if the market/evolutionary mechanisms could in fact capture statistical rational control strategies. The setup consists of a population of firms who are offering a good with a guaranteed quality level, and have a factory routine which delivers the good with a variable quality according to some (unknown) distribution. The firms are created with a fixed advertised quality level and price.

The buyer sets an acceptable quality level and then buys from lowest-priced firm whose advertisement matches. The buyer then raises the quality level to just above the quality of the actual object obtained, and repeats. When the quality desired is higher than any offered, the buyer resets to a low quality level and repeats the entire process.

The desired phenomenon is for the sellers to find appropriate prices for the levels of quality they advertise. This would be done in standard rational control regimes, including our previous work (Hall[97], Steinberg[98]), by taking a statistical sampling of the factory, determining the distribution, and then calculating a price equal to the cost of one factory run divided by the integral of the tail of the distribution above the given quality point, i.e. the expected cost of generating a design of that quality by random probe.

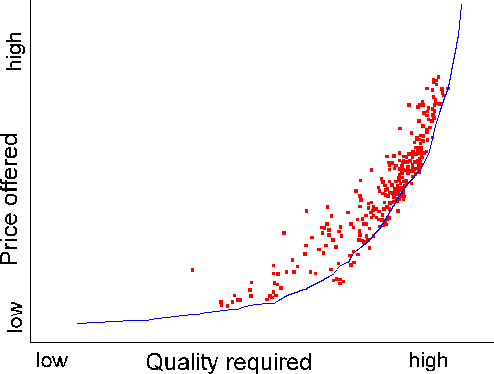
The initial population is distributed uniformly over price/quality space. Firms which offer too low a price/too high a quality will win the bids, run their factories, but rarely have anything to sell, and will lose money from factory running. Firms which offer too high a price/too low a quality will never run, but will lose money more slowly by paying "rent". (It doesn’t really matter in this case what the rent is, since the GA "bankrupts" firms on a relative rather than absolute scale, and any firm making money more slowly than the others is thus at risk). The profitable firms will lie in a band between these regions, as seen here:

Figure 1 Market distribution of firms for a stochastically produced good. The curve represents the calculated rational control locus for optimum utility. Firms below the curve will go bankrupt; competition drives firms above the curve towards it. The curve itself is uneven because it was calculated from (separate) sampling of the factory function. This experiment involved a population size of 300 run for 5000 transactions and 5000 bankruptcies. The scale of the axes is arbitrary within constant factors.

The solid curve in the figure is the set of price/quality relationships given as optimal by our previous statistical method. The width of the band of profitability is determined by the bidding mechanism. The method we use is a tournament from a random sampling of the eligible set. This is "fuzzier" than taking the true global low bid every time, but reflects our model of a real economy where perfect information is not available, and is more suited to distributed implementation.

Subsequent experiments have established that the GA/market mechanism finds the appropriate price levels in the same way in the extended case where there are linear chains of producers and consumers. The model used reflects an abstraction hierarchy in which a given abstract design, say a circuit, can generate many concrete realizations of differing qualities. The value of an abstract design is in the distribution of concrete designs it can generate. The higher abstraction levels sell to the lower ones. First the set of abstraction producers coalesces into a band like the single-stage case, establishing a tacit economic environment where the lower-level buyers can do the same. The random set of purchases made by an uncoalesced buyer population appears to act similarly to the iterative universal buyer in the single-level case. Once the producer population is fairly settled, the secondary population is in essentially the same position, with the difference that the cost of the "factory function", i.e. its real factory plus cost of input, is an additional variable.

A point that we shall return to is the knowledge-rich nature of our GA’s generation function. Our stance on this issue is to import as much knowledge as possible into the model from any source, and to any mechanism, possible. We knew ahead of time that the desired structure of the population in this problem would be in the form of a quasi-linear band in P/Q space, approximating the directly calculated solution. Thus we purposefully used a "crossover" operator that created offspring using a geometric interpretation of the parents’ coordinates (in a cigar-shaped region with one parent at each end). This operator gives the GA a strong propensity to find connected curves; it still has to find the right curve.

Our experience with multiple supplier/consumer chains supports our expectation that when carefully set up, the market converges linearly in the length of the chain. Behavior in the face of loops in the chain is an open question.

Comparing the agoric and statistical models:

• Both models do a fair job of finding the appropriate price for valuations up to the order of 10 times the single-probe cost. Beyond that the statistical method produces less and less reliable estimates of distribution tails (for reasonable sample sizes and well-behaved distributions), but the market method hits a similar limit.
• The market model is more robust in two ways: it does not need a model of the distribution to obtain parameters for; and it doesn't have the "infinite loop" problem where if the distribution used by the statistical method is wrong, and the calculated value is too high, the statistical method can continue probing forever.
• On the other hand, the market model will simply refuse to explore high-risk high-reward parts of the space. This is a tradeoff with "monetary climate" parameters which also determine how fast the initial loose population converges to the equilibrium one. (For fast convergence, our experiments used a climate that causes one bankruptcy per market transaction. As a result, we have a population of very conservative firms.)

Organization under the Price Mechanism into a Productive Structure

Our next experiments moved from abstractional to decompositional structure. In these experiments the firms are manipulating actual layouts. In the first set of experiments we were primarily interested in testing the matching and bidding mechanisms. The primitive modules are introduced into the market by a set of firms, one per type of module. The desired layout was specified by another preset firm which had an unlimited budget and advertised to buy with a spec that the desired layout would satisfy.

In these experiments, since the actual CPU time taken by the office and factory routines was so small, we charged each firm a fixed fee for each, plus an area fee. A more elaborate implementation would have created a different goods type for area, and had a secondary market; but no experimental purpose would have been served in this case. Note that the area charge was only for wasted area at each step; the cost of used area was fully covered by the prices of the input sublayouts.

Each firm (more precisely, the standard office routine) received a list of prices for which each of its desired inputs was available. It made an offer for each spec at a price that was the second lowest (instance, not value) listed price. This is a heuristic inspired by the sealed-bid second-price style of auction, and in practice seems to offer some protection against the relatively common case where the lowest bidder can’t really come up with the goods and is soon to be bankrupt. Each firm then estimates what it must charge for its output at those input prices to remain solvent, and posts that with its output ad.

We generated at random a set of firms which would be capable of constructing the full desired layout, but with prices for inputs and outputs set at random. The resulting market converged to a set of actual transactions, with all prices set appropriately, in between 2 and 3 iterations per depth of the supply-chain tree. The resulting layouts did not differ statistically from randomly generated layouts, having a mean area utilization quotient of about 30%.

In a secondary experiment, we augmented the factory functions with a local optimization technique (essentially, given the inputs, compare all 4 of the locally available options for conjunction for minimum area). Even though prices shifted, convergence did not seem to be materially affected. The resulting layouts were statistically indistinguishable from ones generated by applying the same local optimization using depth-first-search on the layout tree structure, having a mean area utilization quotient of about 60%.

Optimization via Knowledge-based Entrepreneurialism

The first set of experiments was done with fluid sets of firms with fixed prices and specs, and the second set of experiments was done with fixed populations of firms with the ability to adjust their prices. The final set of experiments involved a fluid set of price-adjusting firms. In these experiments we augmented the GA’s breeding mechanism to produce firms that would likely make best use of the available products.

The method was as follows. We generated a secondary lattice relation among specs that could be interpreted "could be a part of", which involved having a subset of the module instances and a "reasonable" size relation. Then we picked at random "Sale" ads in pairs, and compared an estimate of their conjunction, using "could be part of," with "wanted" ads bearing high offered prices. Then, out of the ones that matched, we generated a new firm from the set with the highest estimated profitability. One additional heuristic was to limit new firms to inputs having within a factor of 2 the same number of module instances, since layouts built from one large and one small rectangle tend to be area-inefficient.

The "factory" code of the new firms was simply the local area optimizer run on the inputs it acquired.  Its "wanted" ads were specs copied from the "sale" ads of the "parent" firms (who became its suppliers until some more efficient producer of those subassemblies appeared).  Its sale ad was concocted to specify the smallest output that could be produced given the largest inputs specified by the wanted ads.

The new formulation took much longer for the market to converge, by a full decimal order of magnitude. However, this was to be expected, since the initial market did not actually contain firms capable of producing the desired output whatever their prices. After some experimentation, the overall run worked best when run in three major phases: first, a creation phase where the "breeder" runs alone, initializing a population that is random within its heuristic tendencies. Next, a short purely market phase where price levels are shaken out and producer-consumer chains are established. This phase is equivalent to the entire second experiment, and serves to begin feeding money to the useful firms before the Darwinian elimination begins. Finally, the alternating economic/evolutionary cycle is run for the last overall phase.

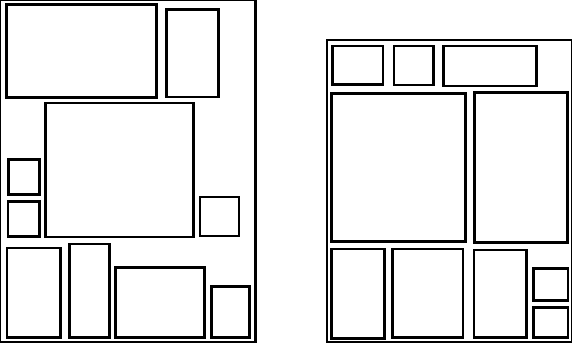
Figure 2: Layouts from the local optimizer (left) and the market system (right) for the same set of primitive modules. The latter was produced in a market which, adding one new firm per cycle, ran for 182 cycles.

The market in this experiment only converged to a smoothly running steady-state economy about half the time. When it did converge, it produced layouts with roughly the same spread of area utilization as the layouts (over the same module sets and tree structures) produced by pure GA’s and random-restart hill climbing, averaging about 90%. However, about one time in ten, the market produced layouts of up to 97% utilization, better than the best from the other methods on the same problems.

Summary of Experiments

This was found to work for three specific coordination tasks: estimation of effort/value ratio in rational control; selection of substructures in a hierarchical design; and generation of new substructures in a hierarchical design.

The experiments also involved a considerable effort by the human experimenter in an exploration of the possibilities of representation and language used by the firms.  We feel that the discovery and demonstration that a lattice (partial ordering) ontological structure is useful and works well in this kind of system is a significant part of our contribution.

We can expect a reasonable amelioration of this phenomenon as experience with the system increases. A better understanding of what is important in the market mechanism will lead to an implementation that leaves some manipulations out and performs the others in a less general way. For example, the system as running now has a major performance improvement over our original implementation that had an advertisement-matching algorithm O(n²) (n the number of firms) at each market cycle; we replaced this with an incremental one which is O(n) at firm creation.

A better understanding of what is important in each kind of design will increase the speed and reliability of the market-level process. For example, early runs of the layout experiment turned out to be taking more market cycles to converge because there was too short a supply of the "raw material" primitive modules. The obvious remedy is to let the primitive suppliers replicate like the transient population. However, as an easy experiment we let them sell duplicate output in a single cycle. This has the undesirable effect, in economic theory, of reducing competition among buyers (every buyer gets a module even though others have offered a lower price). Empirically, however, it speeds up the overall process so much that that effect, if it occurs at all, is swamped, and the market converges an order of magnitude faster on problems where primitive supply was the bottleneck.

Market Convergence

Future Work

Suppose a coin is to be flipped. You should be willing to sell, for $51, a certificate you will redeem for $100 if the coin turns up heads. Similarly you would sell tails certificates. You'd be willing to sell for $2, but not for $3, certificates that paid $100 if a given roll of dice came up "snake eyes". We can regularize this notion into a commodity in units that are certificates that pay one dollar if the fact is true. Clearly a unit of fact F is worth one dollar times the probability of F, and a unit of F and a unit of not(F) in a bundle is worth just a dollar.

These fact futures and the basic operation of price theory (equilibrium price as a function of supply and demand curves) form a method of pooling diverse sources of knowledge of various facts and evolving good estimators. Consider a fact futures market. Over the long run, the following will happen:

• firms which make poor predictions, or bet on facts they don't have any special knowledge of, will go bankrupt.
• firms which spend more to determine the truth of a fact than that knowledge is worth will go bankrupt.

Suppose I am a firm, and I am faced with the option of investing $900 in a product I can sell for $1000 if fact F is true. I can offer to buy 900 units of not(F) for 10 cents apiece. Then if F is true I make $10 net and if not I come out even. This protects me even if I have no idea of the real probability of F. On the other hand, if I'm unable to buy 900 units of not(F) at $0.10, there is no consensus in the market that F is more than 90% likely (e.g. if everyone believes F is only 80% likely, they'll value not(F) at $0.20, and won't sell it for $0.10). In the absence of local knowledge superseding the market, being unable to "fade" the investment bet means the investment is likely counterproductive and shouldn't be pursued.

Chunking and the Firm

In economic theory, the role of the firm is not dissimilar to "chunking" in the AI literature (see Laird, Rosenblum, and Newell [86]). A subsection of the market process is "frozen" into an encapsulated pattern of contractual relationships, eliminating the market overhead for commonly repeated transactions. It is a major goal of the current work to investigate methods for coalescing heavily trafficked subgraphs of the market into firms.

Newell [90] points out a strong similarity in appropriately measured performance between production systems with chunking and human cognitive skills at synthetic reaction-time tasks. This is used as grounds for considering such systems "theories of cognition". There is in economics a phenomenon called the "learning curve" which exhibits essentially the same behavior:

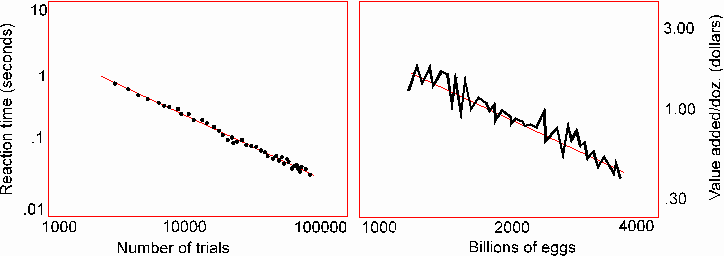
Figure 3: Reaction-time cognitive learning, left, from Newell [90], compared with the economic learning curve, right, from Rothschild [90]. Both show a linear decrease on a log-log scale of resources used in performing a task as a function of the number of task instances performed.
 

Significance of Fact Trading and Chunking

To implement fact trading, we need to do three major things.  First, a language to represent the facts of interest must be invented, and the firms to which the facts are relevant must be written so as to seek the knowledge on the market rather than having built-in search mechanisms.  Secondly, firms that actually discover the facts must be written, and finally, fact traders ("arbitrageurs") must be implemented.  It seems likely that this last, including controlling the behavior the futures market as a dynamic system, is likely to be as great a task as the entire project so far.

Implementation of chunking, in the form of firms "buying up" other firms and thus obviating one or more economic interactions in the productive process, is more straightforward to implement, but the interpretation of price signals as to when and where to do it deserves considerable exploration and experimentation.

If either (or both) of these mechanisms can be made to work in Charles Smith, its learning capabilities would be greatly enhanced.  These appear to be the two learning mechanisms that would integrate most naturally into the market model.
 

Other Open Questions

Secondly, how does the market mechanism itself react to an increased number of firms, and an increased number of different kinds of firms? Can we find distributed algorithms that keep the promise of a highly parallel, decentralized paradigm? What about meta-agents, i.e. allowing the system itself to seek optimal monetary and entrepreneurial policies?
 

There is a well-developed body of work of stochastic methods in design, including GA’s, simulated annealing, random-restart hill-climbing, and so forth. A good overview of their application to the VLSI design problem, as well as specifics of lower-level algorithms and datastructures, can be found in Sherwani [95].

The notion, or at least rigorous analysis, of rational agents in AI architectures is generally traced to Russell and Wefald [91]. Other seminal work involving distributed agents with emphasis on rational allocation of computational resources is Miller and Drexler [88], which explicitly introduced a market model. Our efforts were also influenced by Mitchell and Hofstader [90] to seek a collective mechanism which both translates local decisions into effective global action, and translates global desiderata into comprehensible local conditions. (Although the latter work does not use an explicit market model.)

Agoric and Market-based Algorithms

There is a vast literature in economic simulation, and in economic analysis generally, but we will confine ourselves here to synthetic market systems intended as software architectures for some other purpose than modelling an actual market. These can be broadly classified (by us, not their authors) into two main approaches, the Keynesian and the Austrian. We will refer to as "Keynesian" any system where the agent population is relatively fixed and the main thrust of the mechanism is to seek or maintain a price-theoretic general equilibrium. By far the best developed work in this area is by Wellman et al. in the Walras system (Wellman [95]) and the University of Michigan Digital Library (Mullen [95]). Other work with the Keynesian approach includes the Miller/Drexler proposals and the control systems developed by Waldspurger, Huberman, and Hogg [92].  Most of the systems for allocation (of everything from network bandwidth to pollution permits) discussed in Clearwater[96] would be considered Keynsian under this definition.

We refer to as "Austrian" any approach which relegates market mechanism to the role of informing some other primary metamorphic principle in a relatively plastic population. The seminal instance of this is surely Holland’s original classifier system (Holland [92]), in which the "bucket brigade" approximated a market mechanism in aid of the genetic algorithm. Unfortunately, subsequent work in genetic algorithms seems largely to have abandoned this line of inquiry. A more recent Austrian (explicitly Austrian, by its author) style effort is the Hayek system of Eric Baum [96]. Hayek produces essentially a production system for solving blocks-world problems, using a bidding mechanism to select rules to fire. Although not explicitly genetic, the population is shaped through a Darwinian process of variation and selection.

The notion that markets change by a process resembling Darwinian evolution is by now an accepted part of economic thought; see for example Nelson and Winter [82] and the  Journal of Evolutionary Economics (Springer).  A more empirical exploration is found in Rothschild [90]. That markets form a "discovery procedure" is one of the tenets of the Austrian school of economics; leading thinkers in this school are Hayek and Von Mises. The specific scheme of "fact futures" is adapted from Hanson [95]; an intriguing mapping from the standard equilibrium model and Bayesian inference networks in given in Pennock [96].

Conclusions and Summary of Results

• The combined agoric/genetic method can discover appropriate rational search control functions without prior knowledge of the statistical distributions involved.  (Our related work in rational control, see Steinberg[98], shows that classical rational control given the distributions can cut the amount of search in multi-level design by half.  It remains to be seen whether a large-scale agoric/genetic system can deliver a similar benefit.)
• The language used by the agents in bidding and advertising is of critical importance.  Lattices (partial orderings) on various criteria appear to work well (two -- "better than" and "could be part of" -- being used in the above work).
• The price mechanism can be used to select components and guide the construction of intermediate assemblies. Choosing rationally between custom and stock subdesigns has not yet been shown and will be the subject of future investigations.
• For design, a crucial element in harnessing the market mechanism is eliciting a stream of designs.  Previous work (e.g. Wellman[95]) tried to harness the convergence of the market as an optimization procedure for one design, which appears to preclude combining it with GAs.
• The market/evolutionary mechanism easily accomodates the inclusion of external expertise in a number of forms, including pre-written factories and firms, and sets of concepts present in the advertisement language.

Given an explicit utility for each good for each firm, the problem of finding the optimal set of transactions, in our discrete model that assumes at most one transaction per firm per step, is equivalent to finding a maximal matching in a bipartite graph with weighted edges. In the general case this problem is NP-complete. There are, however, usable heuristics and special cases.

The most commonly treated special case is that in which the goods fall into equivalence classes, such that all goods in a class are valued the same by each firm.

Greedy Optimality for Equivalent Goods

We can produce an optimal set of transactions to be done if all the goods are equivalent. In this case the optimal set of transactions consists of the pairs with positive buyer-seller valuation difference formed by sorting buyers by declining valuation and sellers by increasing valuation, and pairing respectively (the greedy algorithm).

Proof: Call buyers’ utilities b and sellers’ utilities s. The contribution of any pair in the matching to the total increase of utility is b-s. Clearly the b must be higher than any b not in the (optimal) matching and the s must be lower than any s not in the matching (or b1-s or b-s1 would be greater without otherwise changing the matching). Thus the b’s can be divided by a value pb such that all b>pb are in the matching and all b<pb are not. Similarly there is a value ps such that all s<ps are in the matching and all s>ps are not. Note that b>s for any pair in the matching.

If there are no b’s between pb and ps, ps is an equally valid value for pb, and likewise for s’s between ps and pb. Therefore there must be a b and an s between them.

• If pb>ps the b and s are not in the matching (by definition):
• if b>s, b-s should be added, a contradiction.
• if s>b, p = s+b / 2 is a valid value for both pb and ps.
• If ps>pb, b and s are both in the matching (by definition)
• if s>b, the matching contains pairs b0-s and b-s0, but should contain b0-s0, which is greater than the sum of b0-s and b-s0, a contradiction.
• if b>s, p = s+b / 2 is a valid value for both pb and ps.

Therefore there is a single value p for which b>p>s for all paired b and s in an optimal matching (and s>p>b for all unpaired b and s). It does not matter what pairing occurs within this grouping since the total value will be the sum of b’s minus the sum of s’s in any case. The matching found by the greedy algorithm meets this description and has this total value, and is thus optimal, Q.E.D.

Consider next the situation in which the market is complicated by the addition of quality constraints by buyers and sellers. Each individual unit of the good has a quality value. Each buyer has a quality level (in the example, we use ratio of module area to total area) it is willing to accept, and each seller has a quality of the layout it has for sale. There is then a two-dimensional marketplace in which some of the buyers match some of the sellers but it's unlikely that, e.g. the buyer with highest valuation will match the seller with lowest price. In this case the optimal matchup is not so easy to find; the problem is equivalent to finding a maximal matching in a bipartite graph with weighted edges. For a heuristic, we use a method inspired by the one-dimensional case. Simply do transactions in order from highest value difference to lowest.

This is not an optimal solution; consider four firms in (Q,P) space:

• a=(0,10) b=(2,8) buyers
• c=(1,2) d=(3,0) sellers

However, the greedy algorithm is guaranteed to produce at least half the available total utility increase at each step, since each actual transaction can occlude at most two potential transactions, each of which must be of equal or lesser utility than the actual one.

As the characterization of the goods becomes more complex, as in our lattice organization for layouts, or more generally in the interaction between different goods, the problem of finding an optimal matching at each step becomes intractable almost instantly. Furthermore, as the size of the market increases, particularly in a distributed setting, even the greedy algorithm as a heuristic becomes inefficient, requiring us to sort a set of potential transactions that is quadratic in firms and goods.

In our initial implementation, we have used the simple greedy algorithm and suffered the inefficiency, which is not onerous for markets of a few hundred firms, in the interests of expediency. In future, we propose to adopt a scheme based on the sampling and expected value methods of our previous line of investigation.

Each firm, given whatever "advertising" and indexing structures are available, has a local problem in search and expected value. Its probes ("market research") have a certain cost, the market as revealed by this sampling has a certain distribution with respect to expected increase of utility. Each firm, acting locally, can optimize the amount of search it does for "good deals" using a statistics-based rational control algorithm such as that of Hall[97].

Bibliography